命題1４

平方数が平方数を割り切るならば、辺もまた辺を割り切る。辺が辺を割り切るならば、平方数もまた平方数を割り切る。

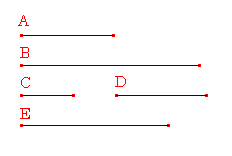
AとBを平方数とし、CとDをそれらの辺とし、AがBを割り切るとする。

CもまたDを割り切ることをいう。

CにDを掛けてEを作る。A、E、BはCがDに対する比において連続して比例している。propositionⅧ．１１

そして、A、E、Bは連続して比例していて、AがBを割り切るから、それゆえにAもまたEを割り切る。そしてAはEに対し同じようにCはDに対し、それゆえにCはDを割り切る。propositionⅧ．７、definitionⅦ．２０

―

次に、CがDを割り切るとする。

AもまたBを割り切ることをいう。

同じ解釈で、A、E、BはCがDに対する比において連続して比例していることを証明で切る。そしてCはDに対し同じようにAはEに対し、そしてCはDを割り切り、それゆえにAもまたEを割り切る。definitionⅦ．２０

そしてA、E、Bは連続して比例していて、AもまたBを割り切る。

それゆえに、平方数が平方数を割り切るならば、辺もまた辺を割り切る。辺が辺を割り切るならば、平方数もまた平方数を割り切る。

証明終了